▲昨天一大早，两个小男孩在玩“哥尼斯堡七桥”。　　记者 王鹏 摄

　　江东百丈街道划船社区荷花庄科普文化公园里，有一条健身路径：几条“小河”隔出了4块陆地，小河上有7座桥将陆地连接。

　　这条看似普通的健身路径却串出了一道世界级的数学难题——怎样才能不重复地走遍这7座桥？

　　为了破解这道难题，自4年前这条健身路径铺成以来，每天都有社区居民在上面反复兜圈，可是至今还没有一个人能找到答案。

　　健身路径吸引居民

　　这条健身路径位于荷花庄公园的广场上，有个很响亮的名字：“哥尼斯堡七桥”。

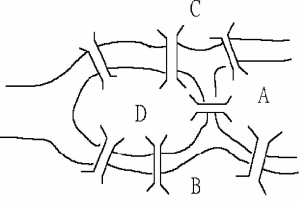
　　整块健身路径设置，看上去非常简单：绿色代表河流，黄色代表陆地，红色代表桥梁，河流的两条分支穿过黄色的陆地，相互交汇，把一整块陆地分成四个部分，在河面上有七座红色的桥，将任意两块陆地连接起来。(如示意图)

　　“桥”和“路”都用石子铺成，人们可以在上面散步，锻炼身体。社区工作人员许文君说，在科普公园里，除哥尼斯堡七桥外，还有麦比乌斯带、立体地形模拟图、分子晶体、科普柱、梦幻魔方等。但从2005年7月科普公园进行改造以来，“哥尼斯堡七桥”最受居民欢迎，每天茶余饭后，不少社区居民就围绕上面的7座“桥”琢磨起来。

　　“七桥”背后隐藏难题

　　“每天在公园里走‘七桥’的居民不少，但很少有人知道在这看似简单的七座桥背后还隐藏着一段故事和一道数学难题。”许文君故作神秘地说，那些居民在上面绕来绕去就是想破解其中的难题。

　　记者上网查阅，与“七桥”相关的资料是这样解释的：相传18世纪，俄国的哥尼斯堡有一条小河叫勒格尔河，河有两条支流，一条叫新河，一条叫旧河，在市中心汇合，在合流的地方中间有一座小岛，在小岛和两条支流上建有七座桥。哥尼斯堡的居民有个传统习惯，星期天沿着城市的河岸和小岛散步，同时试图找出一条路线，可经过所有七桥但又不重复经过任意一座桥，这就成了著名的“七桥问题”。

　　益智游戏其乐无穷

　　刚开始，看着大伙在“哥尼斯堡七桥”上绕来绕去，住在荷花庄的黄老先生还真有点想不明白其中有什么乐趣。一次偶然的机会，他从邻居口中得知其中的“玄机”，也尝试着走了几回。

　　“没想到看上去‘小儿科’的东西，确实还蛮难的。”黄先生心里有点不服输，走了一次又一次，倒走顺走，就是没法不重复走遍七座桥。

　　不过，他一点也不灰心。因为“一边要动脑子，一边脚步要跟上，绕来绕去，运动量也很大，这样既锻炼了身体，又开动了脑筋。”4年来，黄先生一有空就要来走走，乐此不疲。

　　居民们都说在“哥尼斯堡七桥”散步，要比平时一个人默默地沿着街边走更有乐趣。

　　小孩发明其它游戏

　　荷花庄小学三年级学生小魏对“哥尼斯堡七桥”更是情有独钟，几乎每个星期都要拉上小伙伴来这里“过桥”。

　　“我想了很多办法，但最多只能一次过六座桥。”小魏说，有时会让他觉得有些沮丧，但他很快就把这些烦恼抛在脑后，因为他和小伙伴在“哥尼斯堡七桥”上又发明了新的益智游戏，就是如何避免和扮演敌人的小伙伴在同一座桥上“相撞”。

　　-延伸阅读

　　数学专家解读“哥尼斯堡七桥”

　　这个“任务”不可能完成

　　记者就“七桥问题”咨询了宁波大学理学院副院长徐允庆教授，他认为，这是一个不可能完成的“任务”，并对此作出了详细解释。

　　当时瑞士著名数学家欧拉对“七桥问题”也产生了兴趣。欧拉把被河流隔开的小岛和3块陆地看成4个点，把每座桥看成一条线。七桥问题就抽象为4个点和7条线组成的几何图形，数学上称之为网络。于是，“一个人能否无重复地一次走遍七座桥最后回到起点”就变成“从4个点中某一个点出发，能否1笔把这个网络画出来”，这就是所谓的一笔画。

　　欧拉研究发现，网络能否一笔画出来的关键在于这些点。这些点有两类，如果从一点引出的线是奇数条，就把这个点叫奇点；如果从一点引出的线是偶数条，就把这个点叫偶点。网络中奇点的数是零或二，这个网络就能一笔画出来。而“七桥问题”中的4个点都是奇点，按欧拉的规律，这个网络是一笔画不出来的。也就是说想一次无重复地走过所有七座桥是不可能的，因为根本就不存在这样一条路线。（东南商报记者范洪 石承承 通讯员 唐珍洁）