数学
命题意图
数学试题命制以《义务教育数学课程标准（2011年版）》为依据，主要考查“数与代数”“图形与几何”“统计与概率”三个方面的内容，同时将“综合与实践”内容有机融入其中。初中学业水平考试是全面检测学生在初中阶段数学学习水平的最权威的测试，也为高中段的招生提供了客观依据。而考试能否科学全面地评价学生，关键之处就在于能否根据考试的功能编制出源于四基、着眼能力、关注素养、立足发展的试题。所以，命题以四基为本，回归教材，实现对基础知识的全面考查；以方法为脉，串联考点，实现对通性通法的重点考查；以思想为魂，突出本质，实现对综合运用能力的灵活考查；以能力为意，丰富内涵，实现对数学核心素养的有效考查。整份试卷以素养立意，坚持原创，层次分明，亮点纷呈，体现了试题的有效性、导向性、公平性和创新性的和谐统一。
一、立德树人，素养立意
培养学生追求真理、勇于钻研、敢于创新的精神和良好的社会责任感、使命感，促进人的发展是学科育人的终极目标，也是命题者在实践中前行的航标。
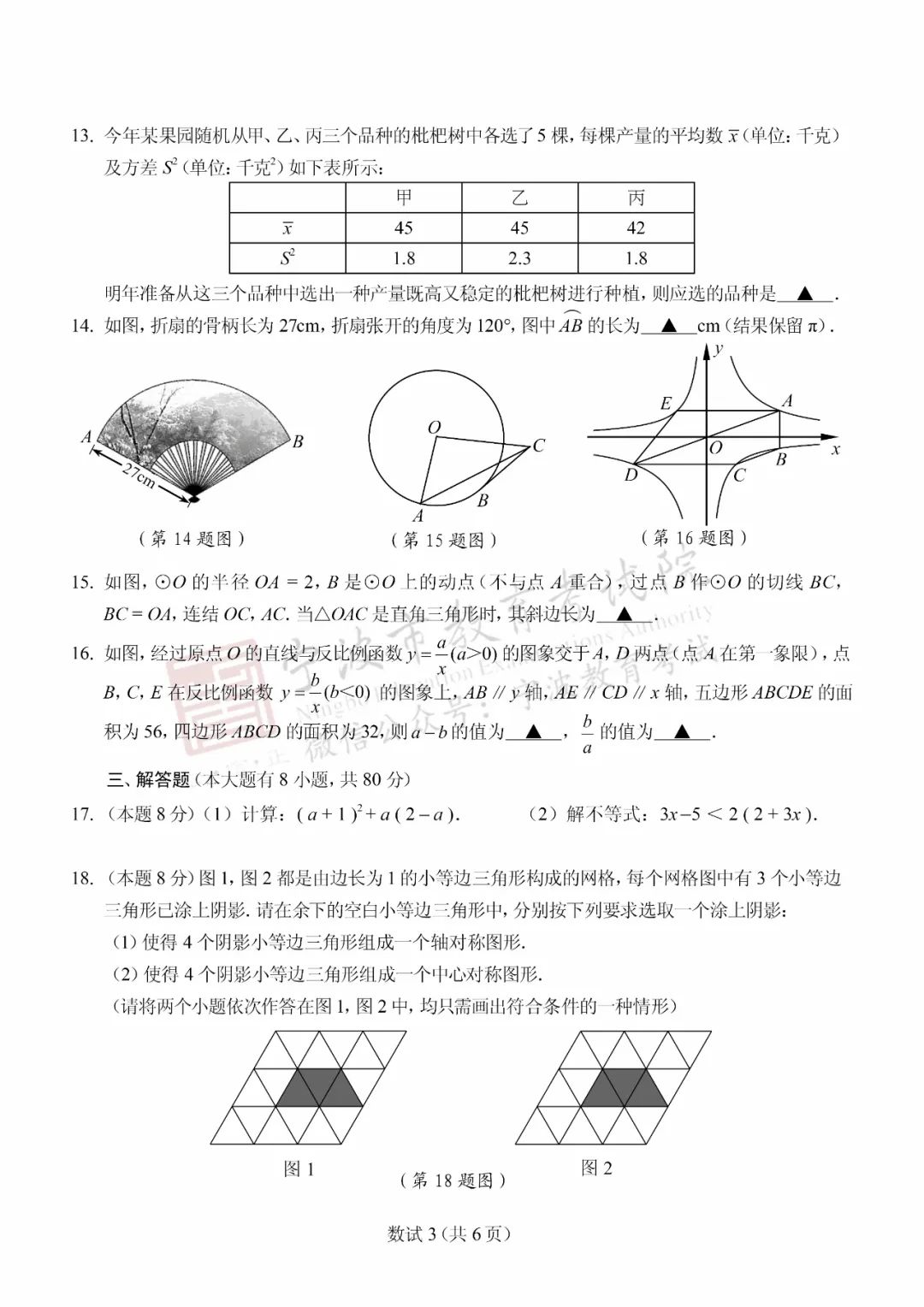
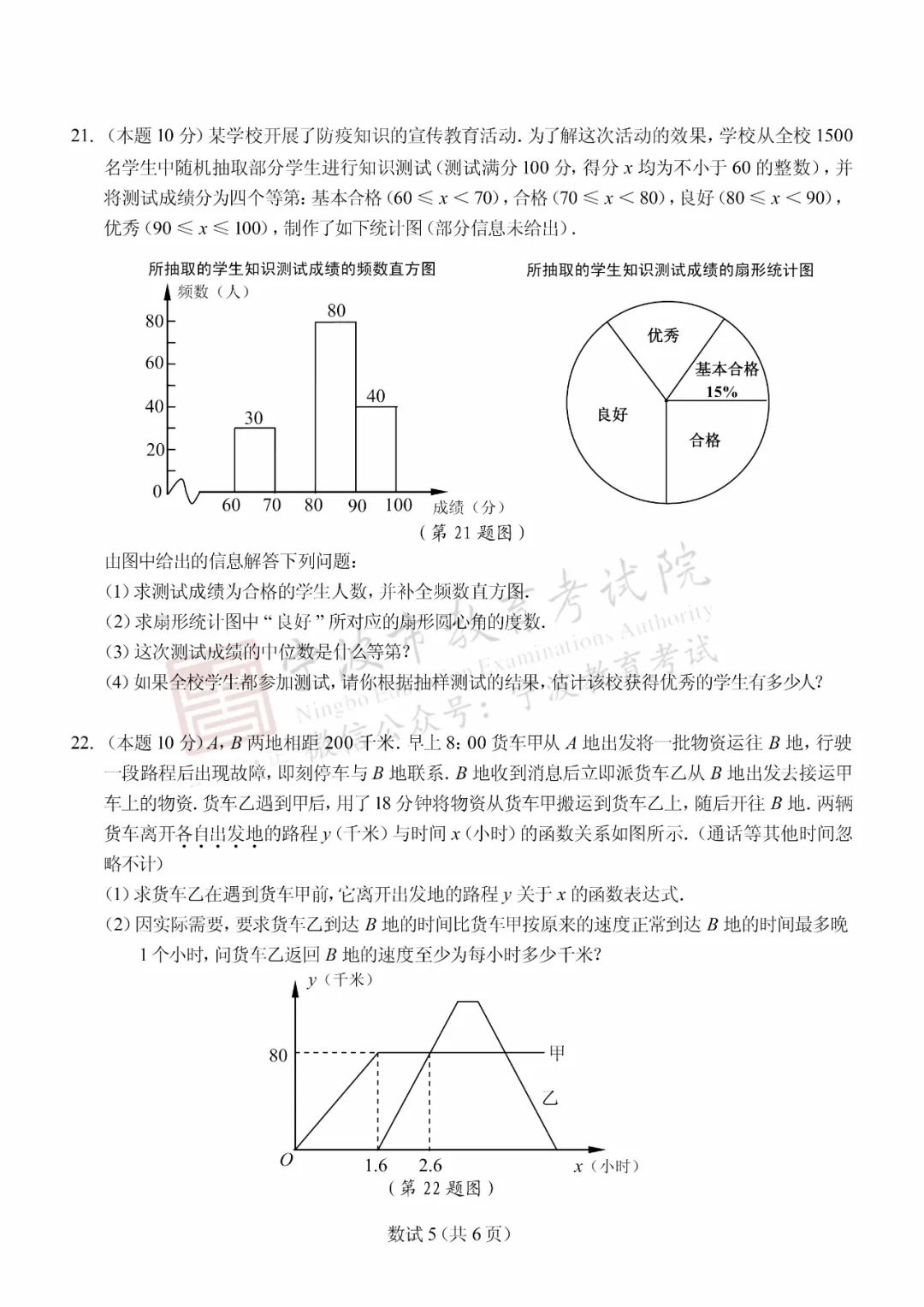
宁波初中学业水平考试数学试题有三大特色题，即PISA试题、新定义试题和实际应用题，今年依然保持这三大亮点。试卷的第10题、第19题是PISA试题，它们具有PISA试题的三大特征，即情景、运用和思维。第10题既可以对全等的三个三角形的边长设元，通过代数式运算得到结果，又可以运用图形变换（移动线段）的方法解答，两种方法均需用到数形结合思想和整体思想，体现了对学生抽象思维、几何直观、数学运算等学科素养以及运用知识解决或解释问题的能力的考查。第19题是在当今社会关注有序停车这个现实背景下，采用生活素材“新型车位锁”并结合PISA理念编制而成的试题，意在考察学生用数学的眼光观察世界（数学抽象和直观想象）、用数学的思维思考世界（逻辑推理和数学运算）、用数学的语言表达世界（数学建模和数据分析）的能力，充分体现了数学与生活的紧密联系，为学生形成良好的数学价值观奠定基础。第21题以学生参与防疫知识宣传教育活动的测试成绩为素材，结合统计图表及中位数等统计量，考查学生分析数据及以样本估计总体解决实际问题的能力。这样的设计对于发展学生的统计思想，培养学生的社会责任感、使命感，体会数学的现实意义有重要作用。
二、回归本源，引领教学
随着课改的深入践行，试题更加注重体现数学学科的本质，准确引领教学的方向。试卷中有相当数量的试题源于教材，是教材中习题的变式、引申与拓展。返璞归真，以突出对数学概念与本质的考查，如第1、4、5、8、10、14、22题等。试卷中有一定数量的试题突出数学基本思想方法的考查，如第10题考查抽象能力、几何直观素养及数形结合、转化思想；第15题依托点的运动变化来考查分类讨论思想；第22题考查数学建模、数形结合的思想等；第10、15、18、23题涉及基本活动经验的考查。这些试题需要学生在思维上真正参与数学活动，积累思考的方式和实践的经验，形成解决问题的方式方法，发展核心素养。这样的设计能充分体现试题的区分度、信度和效度。
今年的试题更关注初高中衔接，加强对一次函数、反比例函数、二次函数概念的理解及性质应用的考查，如第9、16、20、22题。第9题通过对选择支的巧妙设置，实现了对二次函数图像顶点、增减性、对称性及关键点的函数值的综合考查。第22题应用题以学生日常生活中所熟悉的行程问题为背景，实现对一次函数、待定系数法、识图能力、数形结合能力的考查，彰显对数学建模、逻辑推理等核心素养培养的重视。以实际生活问题为背景的试题，在教学中教师需引导学生学会读题和理解题意，并将实际问题“数学化”，运用数学知识解决问题。
三、关注过程，注重创新
《义务教育数学课程标准（2011年版）》指出：数学课程内容“不仅包括数学的结果，也包括数学结果的形成过程和蕴含的数学思想方法”。因此在编制试题时，我们关注过程与方法，凸显对学生学习能力、探究能力的考查。第16题作为填空压轴题，此类型的试题需分析洞察题中各条件，建立条件与条件、条件与结论之间的联系，按正确的方向进行思考探究，这是数学解决问题的一般方法。它的解决需要利用中心对称性先进行面积的等积转化，再结合k的几何意义建立关于“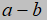
”的方程组，这是解决问题的关键。第23题呈现形式新颖简约，问题设计坡度合理，蕴含丰富的思维含量，且兼顾整体性又对“个性发展”的差异性作出有效甄别。它体现了对“基础巩固—尝试应用—拓展提高”的学习过程的考查，要求学生的学习能够从“知识的回顾”到“本质的理解”，再抵达“灵活应用”的层次，为后续的学习积累重要的学习方法，充分体现数学学习过程的意义。
四、重视应用，凸显能力
为有效遏制题海战术，减轻学生学业负担，试题的命制完全避免模型化套路，注重通性通法，淡化特殊技巧。第24题压轴题以新定义试题形式呈现，表述简洁，内涵丰富。各小题在知识上自然衔接、相互关联，在能力上逐步递进、环环相扣。如此设置梯度明显，有利于不同层次学生的发挥。它以圆为背景，将圆的基本性质与三角形边角关系、三角形全等和相似、勾股定理、三角函数等核心知识融合在一起，体现了函数思想、方程思想、转化思想等数学中重要的思想方法，旨在实现对学生综合运用知识解决问题的能力及学科素养的全面考查。试题真正体现数学逻辑与数学直观的相互交织，立意深刻，要求学生通过阅读理解、推理计算、性质应用等方式进行即时的学习和研究，着重考查数学学习过程与潜能，体现了“知识与能力并重，思想与方法交融”的命题思想，使得压轴题的综合性、公平性和导向性得到充分体现。（命题组）
试题
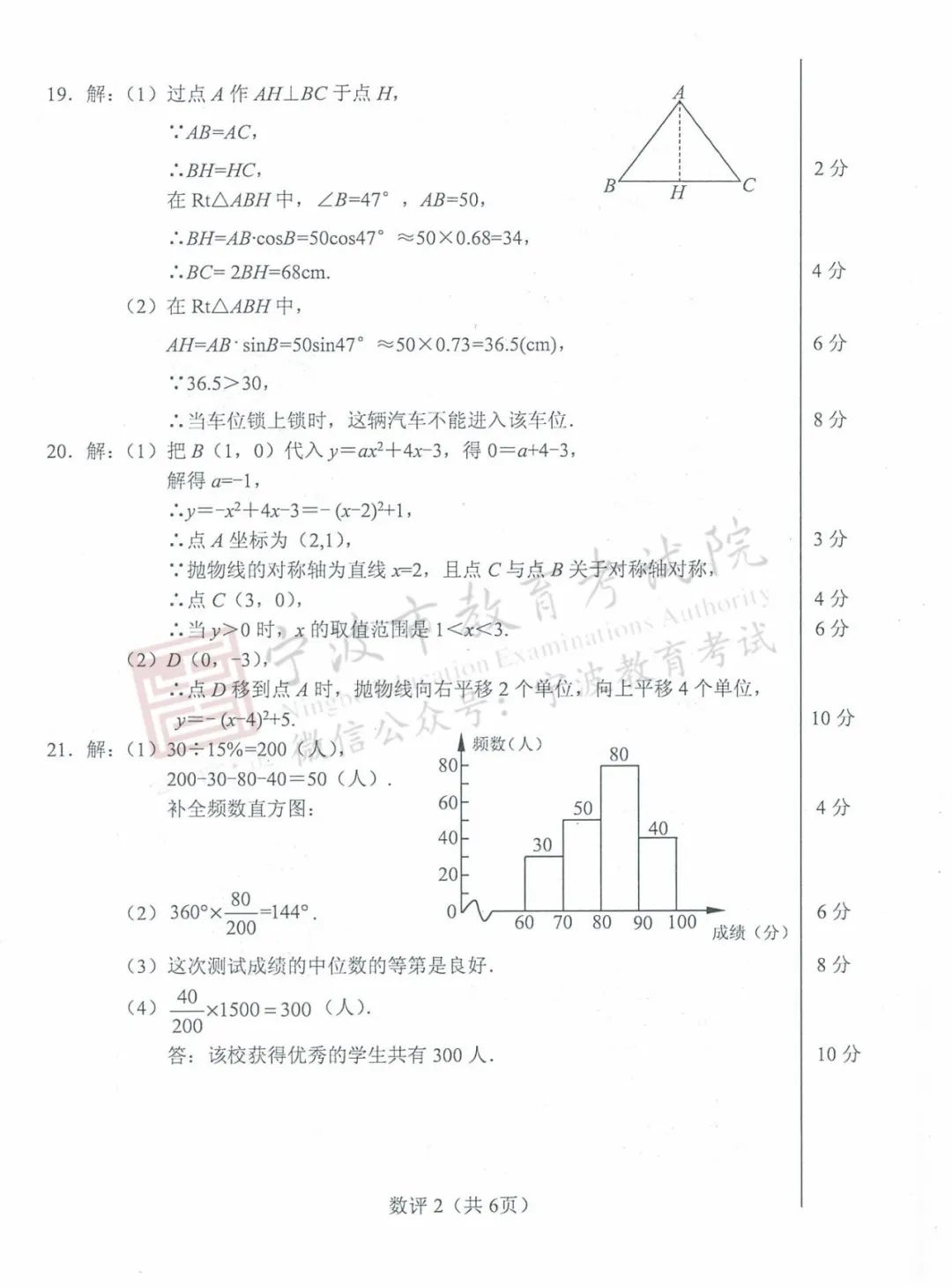
参考答案与评分参考
编辑： 杜寅纠错：171964650@qq.com
