数学
命题意图
数学试题命制以《义务教育数学课程标准》(2011年版)和浙教版六册教材为依据,主要考查“数与代数”、“图形与几何”和“统计与概率”三个方面的内容,同时将“综合与实践”内容有机融入其中。命题以四基为本,回归教材,实现对基础知识的全面考查;以方法为脉,串联考点,实现对通性通法的重点考查;以思想为旨,突出本质,实现对运用能力的综合考查;以能力为意,丰富内涵,实现对数学核心素养的有效考查。整份试卷以素养立意,原创为本,层次分明,亮点纷呈,体现出试题的有效性、导向性、公平性和创新性的和谐统一。
一、素养立意,突出育人价值
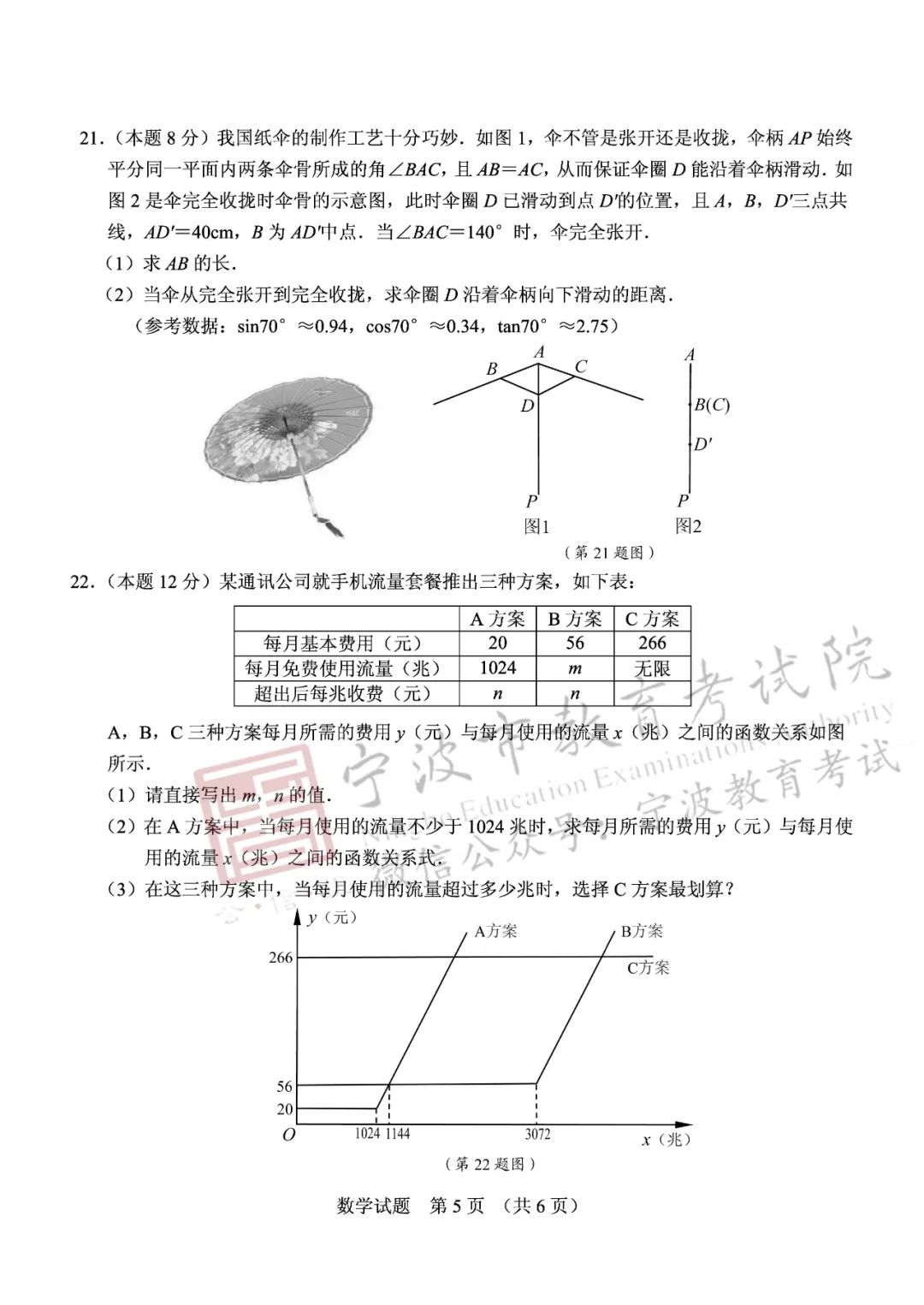
PISA试题、新定义试题、情景应用题、迁移型试题、综合探究题是历年宁波中考数学试题的亮点体现,今年依然多方呈现这些亮点。如第8题依托史料,彰显人文价值。第10题、第21题是PISA试题,它们具有PISA试题的三大特征即:情景、运用和思维。第10题既可以对直角三角形的边长与矩形的边长设元,凸显符号意识,借助代数推理求解;也可以运用几何直观,通过图形变换进行等积转化的方法解答,体现了对学生抽象思维、几何直观、数学运算等学科素养及应用知识解决或解释问题能力的考查。第21题是采用学生生活中熟悉的素材—纸伞并巧妙结合PISA理念命制而成的试题,属于解直角三角形的应用题,命题角度新颖,既贴近生活,又需要借助锐角三角函数,解直角三角形、等腰三角形等数学知识才能解决。它源于教材又高于教材,意在考查学生应用数学的眼光观察世界(数学抽象、直观想象)、用数学的思维思考世界(逻辑推理、数学运算)、用数学的语言表达世界(数学建模、数据分析)的能力,充分体现了数学与生活的紧密联系,为学生形成良好的数学价值观奠定基础。
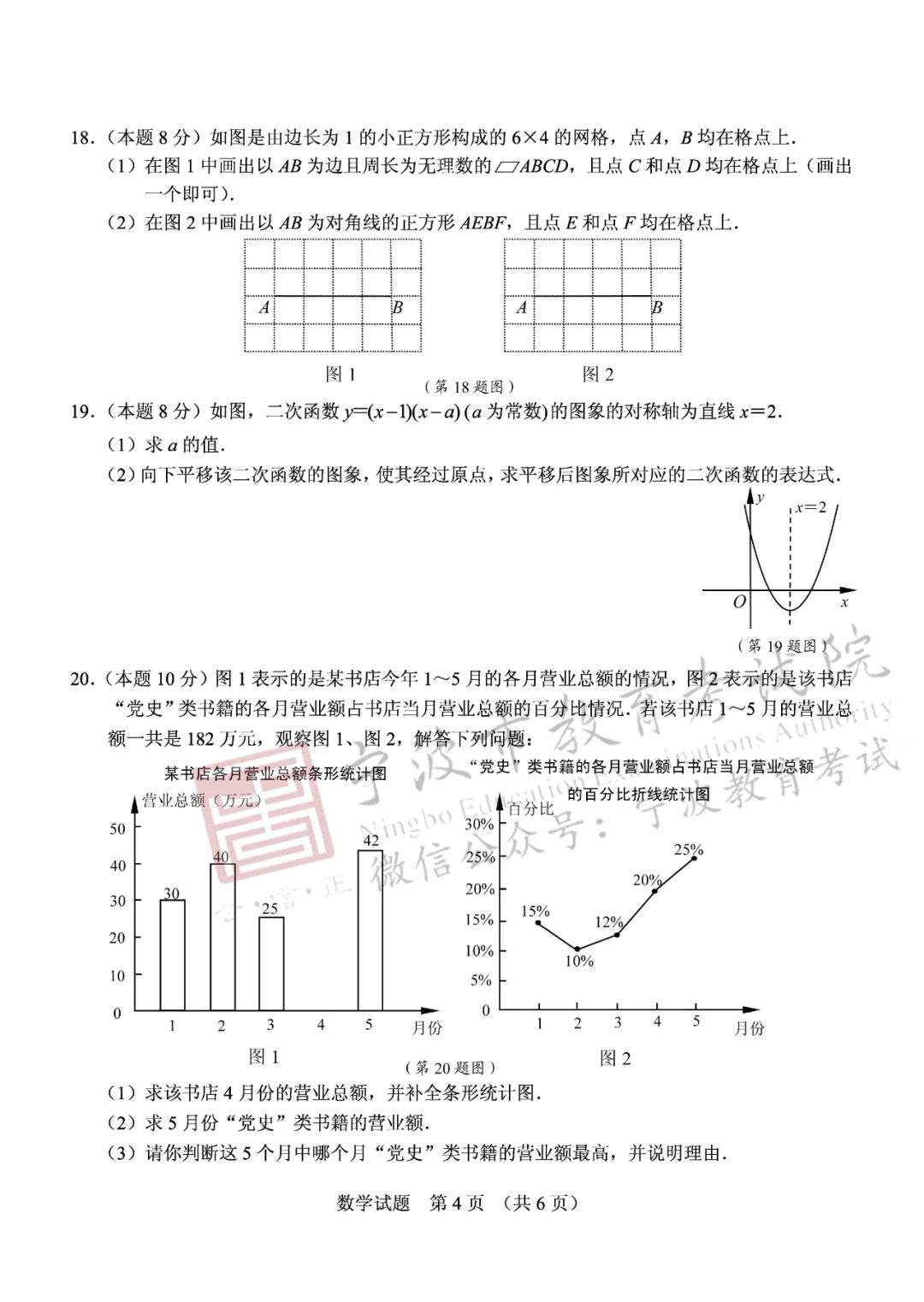
第15题是一道关于“倒数点”的新定义试题,巧妙实现了对反比例函数中k的几何意义及对称性等性质的综合考查,依托点的位置变化来考查分类讨论思想。题在书外,根在书内,朴实于外,灵动于内。第20题以书店红五月党史类书籍热销等营业情况为素材,结合统计图表及相关统计量,考查学生观察数据、分析数据及应用数据分析解决问题的能力。这样的设计对于发展学生的统计思想,培养学生对社会的责任感、使命感,体会数学的现实意义有重要作用。
二、源于教材,引领教学方向
随着课改的深入,试题更加关注数学思想方法的应用,体现数学学科的本质,准确引领教学的方向。试卷中有相当数量的试题源于教材,是教材中习题的变式、引申与拓展,立足基础,体现考试性质;回归教材,导向课堂教学。如此返璞归真,以突出对数学概念与本质的考查,如第1、2、5、6、9、13、14、17、21、22题等;试卷中有一定数量的试题突出数学基本思想方法的考查,如第10题考查抽象能力、几何直观素养及数形结合、转化思想;第22题考查数学建模、数形结合的思想等;第10、15、19、23题涉及基本活动经验的考查,这些试题需要学生思维上真正参与数学活动,积累思考的方式和实践的经验,形成解决问题的方式方法,发展核心素养。这样的设计能充分体现试题的区分度、信度和效度。
今年的试题同样关注初高中衔接,加强对一次函数、反比例函数、二次函数概念的理解及性质应用的考查,如第9、15、19、22题。第22题应用题以学生日常生活中耳闻目见的手机流量问题为背景,实现对一次函数、待定系数法、识图能力、数形结合能力的考查,彰显对数学建模、逻辑推理等核心素养培养的重视。以实际生活问题为背景的试题,在教学中需教师引导学生学会读题和理解题意,并将实际问题“数学化”,运用数学知识解决问题。
三、关注过程,重视数学思考
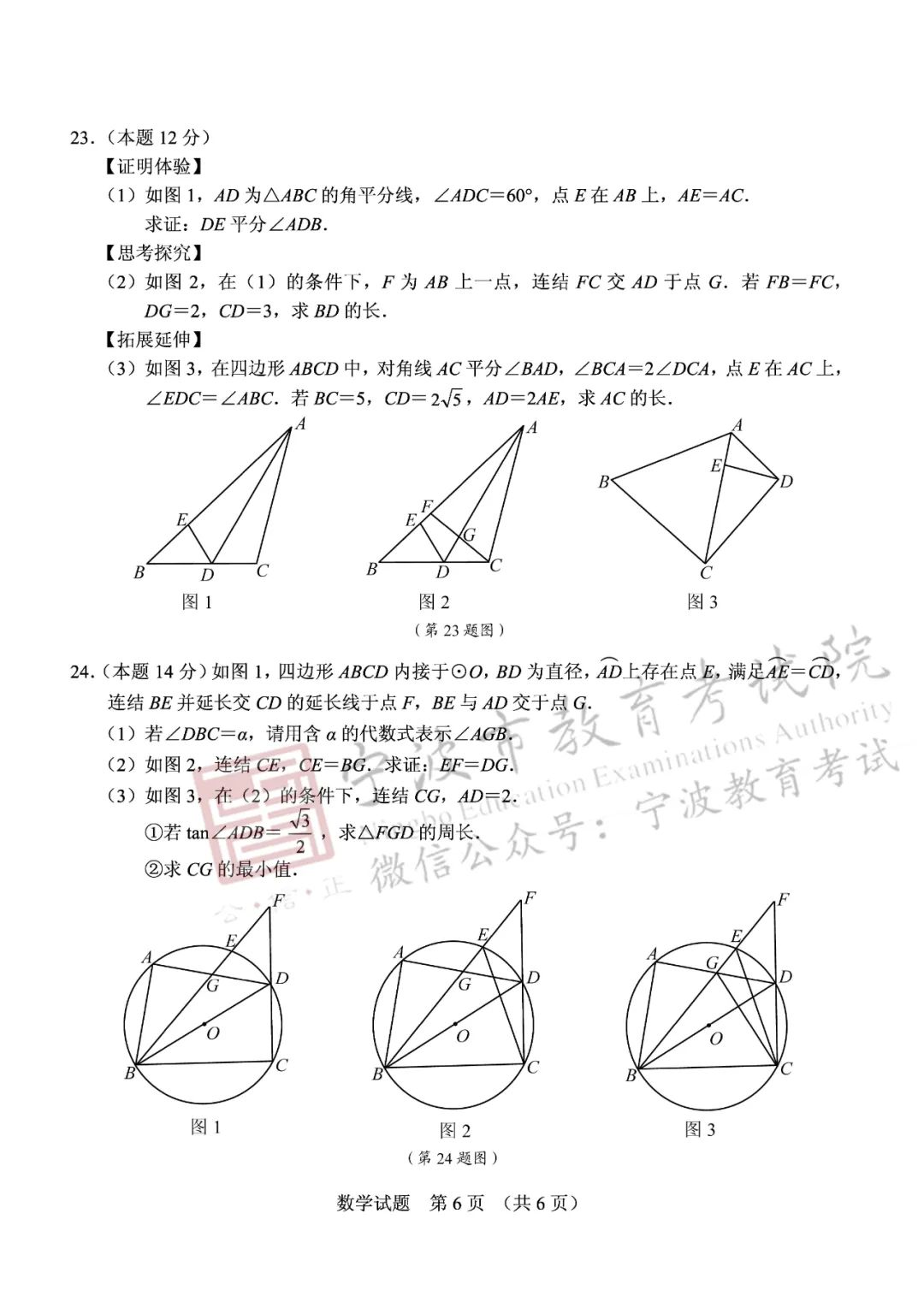
《义务教育数学课程标准(2011版)》指出:“数学课程内容不仅包括数学的结果,也包括数学结果的形成过程和蕴含的数学思想方法。”因此在编制试题时,我们关注过程与方法,凸显对学生学习能力、探究能力的考查。今年首次将新定义问题放置在第15题,以数学概念学习过程为载体考查学生数学学习能力及综合应用能力。第16题其实质是翻折问题,学生因情景熟悉而亲切,但它却是“熟悉的陌生人”。解决该问题需要慧眼识珠,能洞察到题中独特的线段的位置关系和数量关系,建立条件与条件、条件与结论之间的联系,按正确的方向进行思考探究,这是数学解决问题的一般方法。第23题以基础知识与基本结论为载体,梯度进阶,重视迁移,关注过程方法,凸显思维发展,其呈现形式新颖简约,问题设计坡度合理。它体现了从证明体验—思考探究—拓展延伸的学习过程的考查,自然、流畅、质朴、和谐,要求学生的学习能够从“方法的体验”到“本质的理解”再抵达“灵活应用”,为后续的学习积累重要的学习方法,充分体现数学学习过程的意义。
四、重视能力,回归教育本质
为有效遏制题海战术,减轻学生学业负担,试题的命制避免模型化套路,注重通性通法,淡化特殊技巧。第24题呈现简洁新颖,内涵丰富,巧妙避开常规套路。它以圆为背景,将圆的基本性质与三角形边角关系、三角形全等和相似、勾股定理、三角函数等核心知识融合在一起,蕴涵了函数思想、方程思想、转化思想等数学中重要的思想方法,将核心知识和数学思维体现得淋漓尽致,彰显了对数学核心素养的考查要求。在问题设置上层次分明,各小题在知识上自然衔接,相互关联;能力上逐步递进,环环相扣,体现了“平和中见关怀,沉稳中显活力,自然中现宗旨”的命题特点。最后一问对个性发展的差异性作出有效“甄别”,它的求解方法巧妙避开了通常求最值的套路,转为深入挖掘隐含的数量关系,进而通过建立变量之间的函数关系来求解,解法多元,彰显个性,真正体现“知识与能力并重,思想与方法交融”的命题思想,使得压轴题的综合性、创新性、导向性和公平性得到充分体现。
培养学生追求真理,勇于钻研,敢于创新的精神和良好的社会责任感、使命感,促进人的发展是学科育人的终极目标,也是命题人在实践中前行的航标。(命题组)
试题



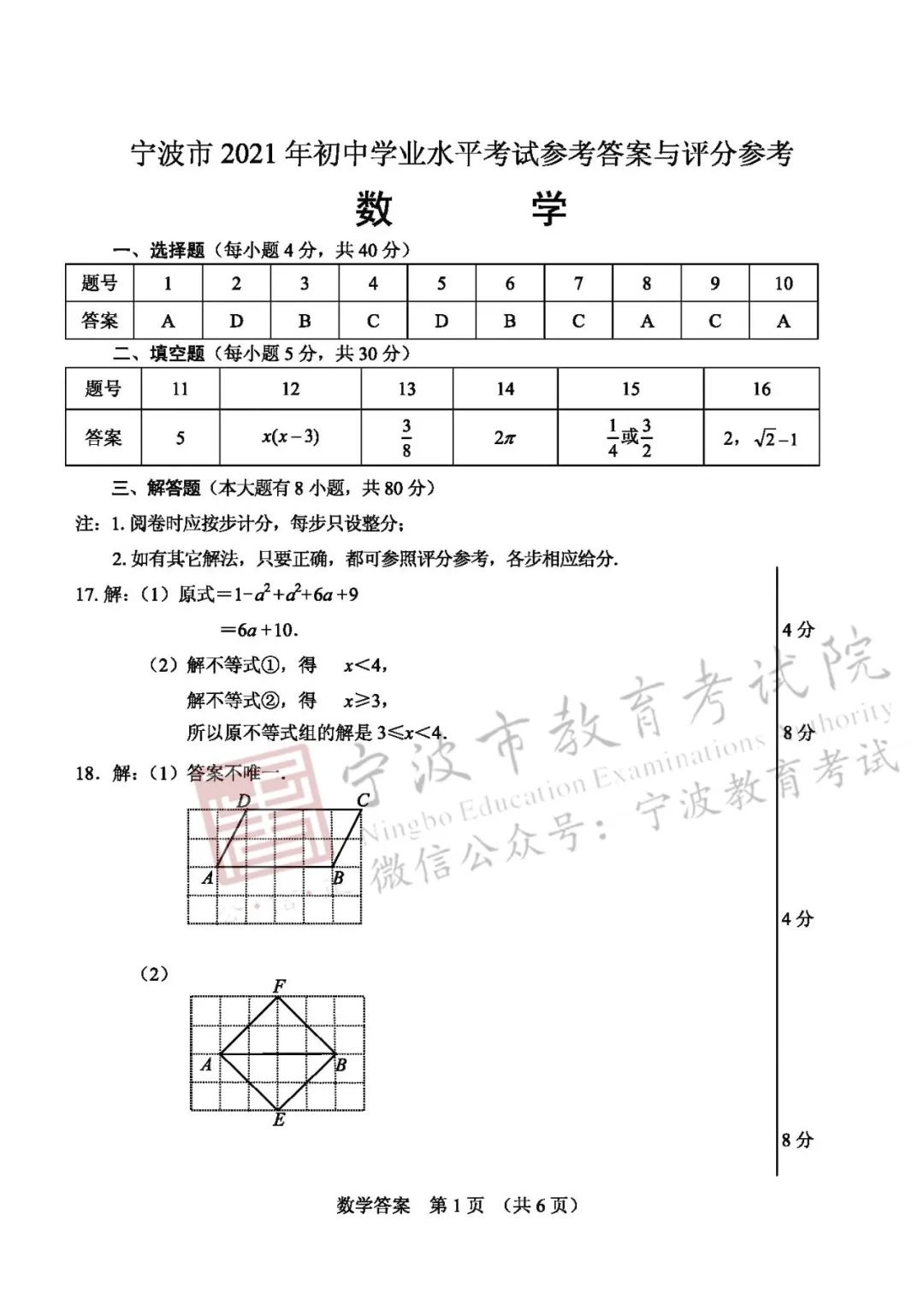
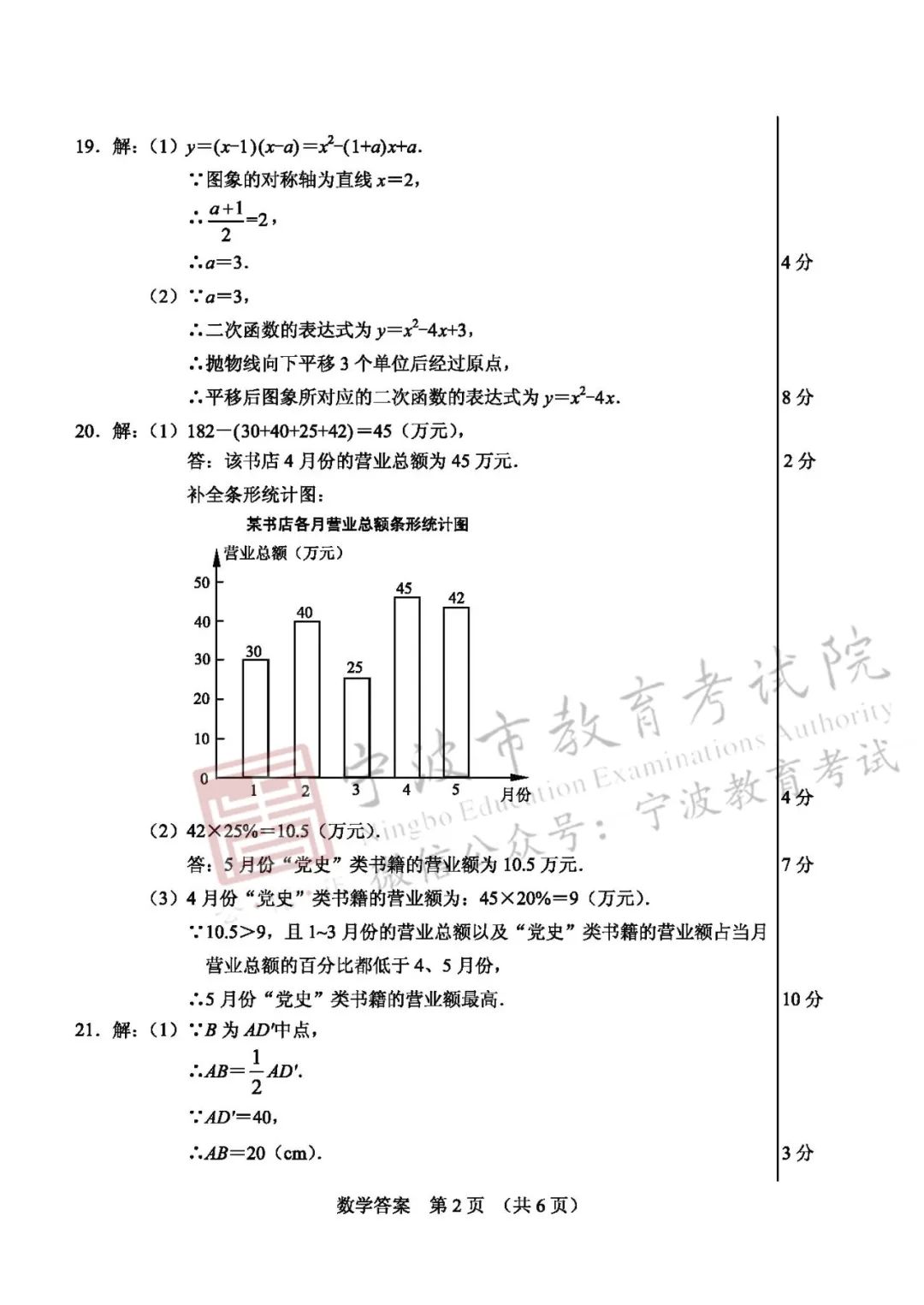
参考答案与评分参考




编辑: 陈捷纠错:171964650@qq.com